Statistical hypothesis testing
A statistical hypothesis test is a method of making decisions using experimental data. In statistics, a result is called statistically significant if it is unlikely to have occurred by chance. The phrase "test of significance" was coined by Ronald Fisher: "Critical tests of this kind may be called tests of significance, and when such tests are available we may discover whether a second sample is or is not significantly different from the first."[1]
Hypothesis testing is sometimes called confirmatory data analysis, in contrast to exploratory data analysis. In frequency probability, these decisions are almost always made using null-hypothesis tests (i.e., tests that answer the question Assuming that the null hypothesis is true, what is the probability of observing a value for the test statistic that is at least as extreme as the value that was actually observed?)[2] One use of hypothesis testing is deciding whether experimental results contain enough information to cast doubt on conventional wisdom.
Statistical hypothesis testing is a key technique of frequentist statistical inference, and is widely used, but also much criticized. While controversial,[3] the Bayesian approach to hypothesis testing is to base rejection of the hypothesis on the posterior probability.[4] Other approaches to reaching a decision based on data are available via decision theory and optimal decisions.
The critical region of a hypothesis test is the set of all outcomes which, if they occur, will lead us to decide that there is a difference. That is, cause the null hypothesis to be rejected in favor of the alternative hypothesis. The critical region is usually denoted by C.
Contents |
Examples
The following examples should solidify these ideas.
Example 1 - Court Room Trial
A statistical test procedure is comparable to a trial; a defendant is considered innocent as long as his guilt is not proven. The prosecutor tries to prove the guilt of the defendant. Only when there is enough charging evidence the defendant is condemned.
In the start of the procedure, there are two hypotheses  : "the defendant is innocent", and
: "the defendant is innocent", and  : "the defendant is guilty". The first one is called null hypothesis, and is for the time being accepted. The second one is called alternative (hypothesis). It is the hypothesis one tries to prove.
: "the defendant is guilty". The first one is called null hypothesis, and is for the time being accepted. The second one is called alternative (hypothesis). It is the hypothesis one tries to prove.
The hypothesis of innocence is only rejected when an error is very unlikely, because one doesn't want to condemn an innocent defendant. Such an error is called error of the first kind (i.e. the condemnation of an innocent person), and the occurrence of this error is controlled to be seldom. As a consequence of this asymmetric behaviour, the error of the second kind (setting free a guilty person), is often rather large.
| Accept Null Hypothesis (H0) Let Him Go |
Reject Null Hypothesis (H0) GUILTY - HANG 'EM HIGH |
|
|---|---|---|
| Null Hypothesis (H0) is true He truly is innocent |
GOOD |
BAD - Incorrectly reject the null Type I Error False Positive |
| Alternative Hypothesis (H1) is true He truly is guilty |
BAD - Incorrectly accept the null Type II Error False Negative |
GOOD |
Example 2 - Clairvoyant Card Game
A person (the subject) is tested for clairvoyance. He is shown the reverse of a randomly chosen play card 25 times and asked which suit it belongs to. The number of hits, or correct answers, is called X.
As we try to find evidence of his clairvoyance, for the time being the null hypothesis is that the person is not clairvoyant. The alternative is, of course: the person is (more or less) clairvoyant.
If the null hypothesis is valid, the only thing the test person can do is guess. For every card, the probability (relative frequency) of guessing correctly is 1/4. If the alternative is valid, the test subject will predict the suit correctly with probability greater than 1/4. We will call the probability of guessing correctly p. The hypotheses, then, are:
- null hypothesis
 (just guessing)
(just guessing)
and
- alternative hypothesis
 (true clairvoyant).
(true clairvoyant).
When the test subject correctly predicts all 25 cards, we will consider him clairvoyant, and reject the null hypothesis. Thus also with 24 or 23 hits. With only 5 or 6 hits, on the other hand, there is no cause to consider him so. But what about 12 hits, or 17 hits? What is the critical number, c, of hits, at which point we consider the subject to be clairvoyant? How do we determine the critical value c? It is obvious that with the choice c=25 (i.e. we only accept clairvoyance when all cards are predicted correctly) we're more critical than with c=10. In the first case almost no test subjects will be recognized to be clairvoyant, in the second case, some number more will pass the test. In practice, one decides how critical one will be. That is, one decides how often one accepts an error of the first kind - a false positive, or Type I error. With c = 25 the probability of such an error is:
and hence, very small. The probability of a false positive is the probability of randomly guessing correctly all 25 times.
Being less critical, with c=10, gives:
Thus, c=10 yields a much greater probability of false positive.
Before the test is actually performed, the desired probability of a Type I error is determined. Typically, values in the range of 1% to 5% are selected. Depending on this desired Type 1 error rate, the critical value c is calculated. For example, if we select an error rate of 1%, c is calculated thus:
From all the numbers c, with this property, we choose the smallest, in order to minimize the probability of a Type II error, a false negative. For the above example, we select:  .
.
| Accept Null Hypothesis (H0) You Believe Subject is Just Guessing Send him home to Mama! |
Reject Null Hypothesis (H0) You Believe Subject is Clairvoyant Take him to the Horse Races! |
|
|---|---|---|
| Null Hypothesis (H0) is true Subject Truly is Just Guessing |
GOOD  |
BAD - Incorrectly reject the null Type I Error False Positive  |
| Alternative Hypothesis (H1) is true Subject is Truly a Gifted Clairvoyant |
BAD - Incorrectly accept the null Type II Error False Negative  |
GOOD  |
But what if the subject did not guess any cards at all? Having zero correct answers is clearly an oddity too. The probability of guessing incorrectly once is equal to p'=(1-p)=3/4. Using the same approach we can calculate that probability of randomly calling all 25 cards wrong is:
This is highly unlikely (less than 1 in a 1000 chance). While the subject can't guess the cards correctly, dismissing H0 in favour of H1 would be an error. In fact, the result would suggest a trait on the subject's part of avoiding calling the correct card. A test of this could be formulated: for a selected 1% error rate the subject would have to answer correctly at least twice, for us to believe that card calling is based purely on guessing.
Example 3 - Radioactive Suitcase
As an example, consider determining whether a suitcase contains some radioactive material. Placed under a Geiger counter, it produces 10 counts per minute. The null hypothesis is that no radioactive material is in the suitcase and that all measured counts are due to ambient radioactivity typical of the surrounding air and harmless objects. We can then calculate how likely it is that we would observe 10 counts per minute if the null hypothesis were true. If the null hypothesis predicts (say) on average 9 counts per minute and a standard deviation of 1 count per minute, then we say that the suitcase is compatible with the null hypothesis (this does not guarantee that there is no radioactive material, just that we don't have enough evidence to suggest there is). On the other hand, if the null hypothesis predicts 3 counts per minute and a standard deviation of 1 count per minute, then the suitcase is not compatible with the null hypothesis, and there are likely other factors responsible to produce the measurements.
The test described here is more fully the null-hypothesis statistical significance test. The null hypothesis represents what we would believe by default, before seeing any evidence. Statistical significance is a possible finding of the test, declared when the observed sample is unlikely to have occurred by chance if the null hypothesis were true. The name of the test describes its formulation and its possible outcome. One characteristic of the test is its crisp decision: to reject or not reject the null hypothesis. A calculated value is compared to a threshold, which is determined from the tolerable risk of error.
| Accept Null Hypothesis (H0) TSA Believes Suitcase contains only Approved Items Allow Person to Board Aircraft |
Reject Null Hypothesis (H0) TSA Believes Suite contains Radioactive Materials Detain at Airport Security |
|
|---|---|---|
| Null Hypothesis (H0) is true Suitcase contains only Approved Items - Clothes, Toothpaste, Shoes... |
GOOD |
BAD - Incorrectly Reject Type I Error False Positive Cavity Searches. Scandal Ensues. Lawsuits to Follow. |
| Alternative Hypothesis (H1) is true Suitcase contains Radioactive Material |
BAD - Incorrectly Accept Type II Error False Negative Terrorist Gets On Board! |
GOOD |
Again, the designer of a statistical test wants to maximize the good probabilities and minimize the bad probabilities.
Example 4 - Lady Tasting Tea
The following example is summarized from Fisher, and is known as the Lady tasting tea example.[5] Fisher thoroughly explained his method in a proposed experiment to test a Lady's claimed ability to determine the means of tea preparation by taste. The article is less than 10 pages in length and is notable for its simplicity and completeness regarding terminology, calculations and design of the experiment. The example is loosely based on an event in Fisher's life. The Lady proved him wrong.[6]
- The null hypothesis was that the Lady had no such ability.
- The test statistic was a simple count of the number of successes in 8 trials.
- The distribution associated with the null hypothesis was the binomial distribution familiar from coin flipping experiments.
- The critical region was the single case of 8 successes in 8 trials based on a conventional probability criterion (< 5%).
- Fisher asserted that no alternative hypothesis was (ever) required.
If and only if the 8 trials produced 8 successes was Fisher willing to reject the null hypothesis – effectively acknowledging the Lady's ability with > 98% confidence (but without quantifying her ability). Fisher later discussed the benefits of more trials and repeated tests.
| Accept Null Hypothesis (H0) Fisher Distrusts Lady. |
Reject Null Hypothesis (H0) Fisher Believes Lady! |
|
|---|---|---|
| Null Hypothesis (H0) is true Lady CANNOT Determine Preparation Method of Tea simply by Tasting it. |
GOOD |
BAD - Incorrectly Reject Type I Error False Positive |
| Alternative Hypothesis (H1) is true Lady CAN Determine Preparation Method of Tea simply by Tasting it. |
BAD - Incorrectly Accept Type II Error False Negative |
GOOD |
The Testing Process
Hypothesis testing is defined by the following general procedure:
- The first step in any hypothesis testing is to state the relevant null and alternative hypotheses to be tested. This is important as mis-stating the hypotheses will muddy the rest of the process.
- The second step is to consider the statistical assumptions being made about the sample in doing the test; for example, assumptions about the statistical independence or about the form of the distributions of the observations. This is equally important as invalid assumptions will mean that the results of the test are invalid.
- Decide which test is appropriate, and stating the relevant test statistic T.
- Derive the distribution of the test statistic under the null hypothesis from the assumptions. In standard cases this will be a well-known result. For example the test statistics may follow a Student's t distribution or a normal distribution.
- The distribution of the test statistic partitions the possible values of T into those for which the null-hypothesis is rejected, the so called critical region, and those for which it is not.
- Compute from the observations the observed value tobs of the test statistic T.
- Decide to either fail to reject the null hypothesis or reject it in favor of the alternative. The decision rule is to reject the null hypothesis H0 if the observed value tobs is in the critical region, and to accept or "fail to reject" the hypothesis otherwise.
It is important to note the philosophical difference between accepting the null hypothesis and simply failing to reject it. The "fail to reject" terminology highlights the fact that the null hypothesis is assumed to be true from the start of the test; if there is a lack of evidence against it, it simply continues to be assumed true. The phrase "accept the null hypothesis" may suggest it has been proved simply because it has not been disproved, a logical fallacy known as the argument from ignorance. Unless a test with particularly high power is used, the idea of "accepting" the null hypothesis may be dangerous. Nonetheless the terminology is prevalent throughout statistics, where its meaning is well understood.
Definition of terms
The following definitions are mainly based on the exposition in the book by Lehmann and Romano:[7]
- Simple hypothesis
- Any hypothesis which specifies the population distribution completely.
- Composite hypothesis
- Any hypothesis which does not specify the population distribution completely.
- Statistical test
- A decision function that takes its values in the set of hypotheses.
- Region of acceptance
- The set of values for which we fail to reject the null hypothesis.
- Region of rejection / Critical region
- The set of values of the test statistic for which the null hypothesis is rejected.
- Power of a test (1 − β)
- The test's probability of correctly rejecting the null hypothesis. The complement of the false negative rate, β.
- Size / Significance level of a test (α)
- For simple hypotheses, this is the test's probability of incorrectly rejecting the null hypothesis. The false positive rate. For composite hypotheses this is the upper bound of the probability of rejecting the null hypothesis over all cases covered by the null hypothesis.
- Most powerful test
- For a given size or significance level, the test with the greatest power.
- Uniformly most powerful test (UMP)
- A test with the greatest power for all values of the parameter being tested.
- Consistent test
- When considering the properties of a test as the sample size grows, a test is said to be consistent if, for a fixed size of test, the power against any fixed alternative approaches 1 in the limit.[8]
- Unbiased test
- For a specific alternative hypothesis, a test is said to be unbiased when the probability of rejecting the null hypothesis is not less than the significance level when the alternative is true and is less than or equal to the significance level when the null hypothesis is true.
- Conservative test
- A test is conservative if, when constructed for a given nominal significance level, the true probability of incorrectly rejecting the null hypothesis is never greater than the nominal level.
- Uniformly most powerful unbiased (UMPU)
- A test which is UMP in the set of all unbiased tests.
- p-value
- The probability, assuming the null hypothesis is true, of observing a result at least as extreme as the test statistic.
Interpretation
The direct interpretation is that if the p-value is less than the required significance level, then we say the null hypothesis is rejected at the given level of significance. Criticism on this interpretation can be found in the corresponding section.
Common test statistics
In the table below, the symbols used are defined at the bottom of the table. Many other tests can be found in other articles.
| Name | Formula | Assumptions or notes | |||
|---|---|---|---|---|---|
| One-sample z-test |  |
(Normal population or n > 30) and σ known. (z is the distance from the mean in relation to the standard deviation of the mean). For non-normal distributions it is possible to calculate a minimum proportion of a population that falls within k standard deviations for any k (see: Chebyshev's inequality). |
|||
| Two-sample z-test |  |
Normal population and independent observations and σ1 and σ2 are known | |||
| Two-sample pooled t-test, equal variances* |  |
(Normal populations or n1 + n2 > 40) and independent observations and σ1 = σ2 and σ1 and σ2 unknown | |||
| Two-sample unpooled t-test, unequal variances* |  |
(Normal populations or n1 + n2 > 40) and independent observations and σ1 ≠ σ2 and σ1 and σ2 unknown | |||
| One-proportion z-test |  |
n .p0 > 10 and n (1 − p0) > 10 and it is a SRS (Simple Random Sample), see notes. | |||
Two-proportion z-test, pooled for  |

|
n1 p1 > 5 and n1(1 − p1) > 5 and n2 p2 > 5 and n2(1 − p2) > 5 and independent observations, see notes. | |||
Two-proportion z-test, unpooled for  |
 |
n1 p1 > 5 and n1(1 − p1) > 5 and n2 p2 > 5 and n2(1 − p2) > 5 and independent observations, see notes. | |||
| One-sample chi-square test |  |
One of the following
• All expected counts are at least 5 • All expected counts are > 1 and no more that 20% of expected counts are less than 5 |
|||
| *Two-sample F test for equality of variances | 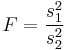 |
Arrange so 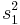 > > 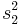 and reject H0 for and reject H0 for  [11] [11] |
|||
In general, the subscript 0 indicates a value taken from the null hypothesis, H0, which should be used as much as possible in constructing its test statistic. ... Definitions of other symbols:
|
|||||
Origins
Hypothesis testing is largely the product of Ronald Fisher, Jerzy Neyman, Karl Pearson and (son) Egon Pearson. Fisher was an agricultural statistician who emphasized rigorous experimental design and methods to extract a result from few samples assuming Gaussian distributions. Neyman (who teamed with the younger Pearson) emphasized mathematical rigor and methods to obtain more results from many samples and a wider range of distributions. Modern hypothesis testing is an (extended) hybrid of the Fisher vs Neyman/Pearson formulation, methods and terminology developed in the early 20th century.
Importance
Statistical hypothesis testing plays an important role in the whole of statistics and in statistical inference. For example, Lehmann (1992) in a review of the fundamental paper by Neyman and Pearson (1933) says: "Nevertheless, despite their shortcomings, the new paradigm formulated in the 1933 paper, and the many developments carried out within its framework continue to play a central role in both the theory and practice of statistics and can be expected to do so in the foreseeable future".
Potential misuse
One of the more common problems in significance testing is the tendency for multiple comparisons to yield spurious significant differences even where the null hypothesis is true. For instance, in a study of twenty comparisons, using an α-level of 5%, one comparison will likely yield a significant result despite the null hypothesis being true. In these cases p-values are adjusted in order to control either the familywise error rate or the false discovery rate.
Yet another common pitfall often happens when a researcher writes the qualified statement "we found no statistically significant difference," which is then misquoted by others as "they found that there was no difference." Actually, statistics cannot be used to prove that there is exactly zero difference between two populations. Failing to find evidence that there is a difference does not constitute evidence that there is no difference. This principle is sometimes described by the maxim "Absence of evidence is not evidence of absence."[12]
According to J. Scott Armstrong, attempts to educate researchers on how to avoid pitfalls of using statistical significance have had little success. In the papers "Significance Tests Harm Progress in Forecasting,"[13] and "Statistical Significance Tests are Unnecessary Even When Properly Done,"[14] Armstrong makes the case that even when done properly, statistical significance tests are of no value. A number of attempts failed to find empirical evidence supporting the use of significance tests. Tests of statistical significance are harmful to the development of scientific knowledge because they distract researchers from the use of proper methods. Armstrong suggests authors should avoid tests of statistical significance; instead, they should report on effect sizes, confidence intervals, replications/extensions, and meta-analyses.
Criticism
Significance and practical importance
A common misconception is that a statistically significant result is always of practical significance, or demonstrates a large effect in the population. Unfortunately, this problem is commonly encountered in scientific writing.[15] Given a sufficiently large sample, extremely small and non-notable differences can be found to be statistically significant, and statistical significance says nothing about the practical significance of a difference.
Use of the statistical significance test has been called seriously flawed and unscientific by authors Deirdre McCloskey and Stephen Ziliak. They point out that "insignificance" does not mean unimportant, and propose that the scientific community should abandon usage of the test altogether, as it can cause false hypotheses to be accepted and true hypotheses to be rejected.[15][16]
Some statisticians have commented that pure "significance testing" has what is actually a rather strange goal of detecting the existence of a "real" difference between two populations. In practice a difference can almost always be found given a large enough sample. The typically more relevant goal of science is a determination of causal effect size. The amount and nature of the difference, in other words, is what should be studied.[17] Many researchers also feel that hypothesis testing is something of a misnomer. In practice a single statistical test in a single study never "proves" anything.[18]
An additional problem is that frequentist analyses of p-values are considered by some to overstate "statistical significance".[19][20] See Bayes factor for details..
Meta-criticism
The criticism here is of the application, or of the interpretation, rather than of the method. Attacks and defenses of the null-hypothesis significance test are collected in Harlow et al..[21]
The original purposes of Fisher's formulation, as a tool for the experimenter, was to plan the experiment and to easily assess the information content of the small sample. There is little criticism, Bayesian in nature, of the formulation in its original context.
In other contexts, complaints focus on flawed interpretations of the results and over-dependence/emphasis on one test.
Numerous attacks on the formulation have failed to supplant it as a criterion for publication in scholarly journals. The most persistent attacks originated from the field of Psychology. After review, the American Psychological Association did not explicitly deprecate the use of null-hypothesis significance testing, but adopted enhanced publication guidelines which implicitly reduced the relative importance of such testing.
The International Committee of Medical Journal Editors recognizes an obligation to publish negative (not statistically significant) studies under some circumstances.
The applicability of the null-hypothesis testing to the publication of observational (as contrasted to experimental) studies is doubtful.
Philosophical criticism
Philosophical criticism to hypothesis testing includes consideration of borderline cases. Any process that produces a crisp decision from uncertainty is subject to claims of unfairness near the decision threshold. (Consider close election results.) The premature death of a laboratory rat during testing can impact doctoral theses and academic tenure decisions.
"... surely, God loves the .06 nearly as much as the .05"[22]
The statistical significance required for publication has no mathematical basis, but is based on long tradition.
"It is usual and convenient for experimenters to take 5% as a standard level of significance, in the sense that they are prepared to ignore all results which fail to reach this standard, and, by this means, to eliminate from further discussion the greater part of the fluctuations which chance causes have introduced into their experimental results."[5]
Ambivalence attacks all forms of decision making. A mathematical decision-making process is attractive because it is objective and transparent. It is repulsive because it allows authority to avoid taking personal responsibility for decisions.
Pedagogic criticism
Pedagogic criticism of the null-hypothesis testing includes the counter-intuitive formulation, the terminology and confusion about the interpretation of results.
"Despite the stranglehold that hypothesis testing has on experimental psychology, I find it difficult to imagine a less insightful means of transiting from data to conclusions."[23]
Students find it difficult to understand the formulation of statistical null-hypothesis testing. In rhetoric, examples often support an argument, but a mathematical proof "is a logical argument, not an empirical one". A single counterexample results in the rejection of a conjecture. Karl Popper defined science by its vulnerability to disproof by data. Null-hypothesis testing shares the mathematical and scientific perspective rather than the more familiar rhetorical one. Students expect hypothesis testing to be a statistical tool for illumination of the research hypothesis by the sample; it is not. The test asks indirectly whether the sample can illuminate the research hypothesis.
Students also find the terminology confusing. While Fisher disagreed with Neyman and Pearson about the theory of testing, their terminologies have been blended. The blend is not seamless or standardized. While this article teaches a pure Fisher formulation, even it mentions Neyman and Pearson terminology (Type II error and the alternative hypothesis). The typical introductory statistics text is less consistent. The Sage Dictionary of Statistics would not agree with the title of this article, which it would call null-hypothesis testing.[2] "...there is no alternate hypothesis in Fisher's scheme: Indeed, he violently opposed its inclusion by Neyman and Pearson."[24] In discussing test results, "significance" often has two distinct meanings in the same sentence; One is a probability, the other is a subject-matter measurement (such as currency). The significance (meaning) of (statistical) significance is significant (important).
There is widespread and fundamental disagreement on the interpretation of test results.
"A little thought reveals a fact widely understood among statisticians: The null hypothesis, taken literally (and that's the only way you can take it in formal hypothesis testing), is almost always false in the real world.... If it is false, even to a tiny degree, it must be the case that a large enough sample will produce a significant result and lead to its rejection. So if the null hypothesis is always false, what's the big deal about rejecting it?"[24] (The above criticism only applies to point hypothesis tests. If one were testing, for example, whether a parameter is greater than zero, it would not apply.)
"How has the virtually barren technique of hypothesis testing come to assume such importance in the process by which we arrive at our conclusions from our data?"[23]
Null-hypothesis testing just answers the question of "how well the findings fit the possibility that chance factors alone might be responsible."[2]
Null-hypothesis significance testing does not determine the truth or falsity of claims. It determines whether confidence in a claim based solely on a sample-based estimate exceeds a threshold. It is a research quality assurance test, widely used as one requirement for publication of experimental research with statistical results. It is uniformly agreed that statistical significance is not the only consideration in assessing the importance of research results. Rejecting the null hypothesis is not a sufficient condition for publication.
"Statistical significance does not necessarily imply practical significance!"[25]
Practical criticism
Practical criticism of hypothesis testing includes the sobering observation that published test results are often contradicted. Mathematical models support the conjecture that most published medical research test results are flawed. Null-hypothesis testing has not achieved the goal of a low error probability in medical journals.[26][27]
Straw man
Hypothesis testing is controversial when the alternative hypothesis is suspected to be true at the outset of the experiment, making the null hypothesis the reverse of what the experimenter actually believes; it is put forward as a straw man only to allow the data to contradict it. Many statisticians have pointed out that rejecting the null hypothesis says nothing or very little about the likelihood that the null is true. Under traditional null hypothesis testing, the null is rejected when the conditional probability P(Data as or more extreme than observed | Null) is very small, say 0.05. However, some say researchers are really interested in the probability P(Null | Data as actually observed) which cannot be inferred from a p-value: some like to present these as inverses of each other but the events "Data as or more extreme than observed" and "Data as actually observed" are very different. In some cases , P(Null | Data) approaches 1 while P(Data as or more extreme than observed | Null) approaches 0, in other words, we can reject the null when it's virtually certain to be true. For this and other reasons, Gerd Gigerenzer has called null hypothesis testing "mindless statistics"[28] while Jacob Cohen described it as a ritual conducted to convince ourselves that we have the evidence needed to confirm our theories.[29]
Bayesian criticism
Bayesian statisticians reject classical null hypothesis testing, since it violates the Likelihood principle and is thus incoherent and leads to sub-optimal decision-making. The Jeffreys–Lindley paradox illustrates this. Along with many frequentist statisticians, Bayesians prefer to provide an estimate, along with a confidence interval, (although Bayesian confidence intervals are different from classical ones). Some Bayesians (James Berger in particular) have developed Bayesian hypothesis testing methods, though these are not accepted by all Bayesians (notably, Andrew Gelman). Given a prior probability distribution for one or more parameters, sample evidence can be used to generate an updated posterior distribution. In this framework, but not in the null hypothesis testing framework, it is meaningful to make statements of the general form "the probability that the true value of the parameter is greater than 0 is p". According to Bayes' theorem, we have:
thus P(Null | Data) may approach 1 while P(Data | Null) approaches 0 only when P(Null)/P(Data) approaches infinity, i.e. (for instance) when the a priori probability of the null hypothesis, P(Null), is also approaching 1, while P(Data) approaches 0: then P(Data | Null) is low because we have extremely unlikely data, but the Null hypothesis is extremely likely to be true.
Publication bias
In 2002, a group of psychologists launched a new journal dedicated to experimental studies in psychology which support the null hypothesis. The Journal of Articles in Support of the Null Hypothesis (JASNH) was founded to address a scientific publishing bias against such articles. According to the editors,
- "other journals and reviewers have exhibited a bias against articles that did not reject the null hypothesis. We plan to change that by offering an outlet for experiments that do not reach the traditional significance levels (p < 0.05). Thus, reducing the file drawer problem, and reducing the bias in psychological literature. Without such a resource researchers could be wasting their time examining empirical questions that have already been examined. We collect these articles and provide them to the scientific community free of cost."
The "File Drawer problem" is a problem that exists due to the fact that academics tend not to publish results that indicate the null hypothesis could not be rejected. This does not mean that the relationship they were looking for did not exist, but it means they couldn't prove it. Even though these papers can often be interesting, they tend to end up unpublished, in "file drawers."
Ioannidis has inventoried factors that should alert readers to risks of publication bias.[27]
Improvements
Jones and Tukey suggested a modest improvement in the original null-hypothesis formulation to formalize handling of one-tail tests. Fisher ignored the 8-failure case (equally improbable as the 8-success case) in the example test involving tea, which altered the claimed significance by a factor of 2[30].
See also
- Comparing means test decision tree
- Counternull
- Multiple comparisons
- Omnibus test
- Behrens–Fisher problem
- Bootstrapping (statistics)
- Checking if a coin is fair
- Falsifiability
- Fisher's method for combining independent tests of significance
- Null hypothesis
- P-value
- Statistical theory
- Statistical significance
- Type I error, Type II error
- Exact test
References
- ↑ R. A. Fisher (1925). Statistical Methods for Research Workers, Edinburgh: Oliver and Boyd, 1925, p.43.
- ↑ 2.0 2.1 2.2 Cramer, Duncan; Dennis Howitt (2004). The Sage Dictionary of Statistics. p. 76. ISBN 076194138X.
- ↑ Spiegelhalter, D. and Rice, K: (2009) Bayesian statistics Scholarpedia, 4(8):5230
- ↑ Schervish, M: Theory of Statistics, page 218. Springer, 1995
- ↑ 5.0 5.1 Fisher, Sir Ronald A. (1956) [1935]. "Mathematics of a Lady Tasting Tea". In James Roy Newman. The World of Mathematics, volume 3 [Design of Experiments]. Courier Dover Publications. ISBN 9780486411514. http://books.google.com/?id=oKZwtLQTmNAC&pg=PA1512&dq=%22mathematics+of+a+lady+tasting+tea%22..
- ↑ Box, Joan Fisher (1978). R.A. Fisher, The Life of a Scientist. New York: Wiley. p. 134.
- ↑ Lehmann, E.L.; Joseph P. Romano (2005). Testing Statistical Hypotheses (3E ed.). New York: Springer. ISBN 0387988645.
- ↑ Cox, D.R.; D.V. Hinkley (1974). Theoretical Statistics. ISBN 0412124293.
- ↑ NIST handbook: Two-Sample t-Test for Equal Means
- ↑ Ibid.
- ↑ NIST handbook: F-Test for Equality of Two Standard Deviations (should say "Variances")
- ↑ BMJ 1995;311:485. Statistics notes: "Absence of evidence is not evidence of absence". Douglas G Altman, J Martin Bland.
- ↑ Armstrong, J. Scott (2007). "Significance tests harm progress in forecasting". International Journal of Forecasting 23: 321–327. doi:10.1016/j.ijforecast.2007.03.004.
- ↑ Armstrong, J. Scott (2007). "Statistical Significance Tests are Unnecessary Even When Properly Done". International Journal of Forecasting 23: 335–336. doi:10.1016/j.ijforecast.2007.01.010.
- ↑ 15.0 15.1 Ziliak, Stephen T. and Deirdre N. McCloskey.(2004) "Size Matters: The Standard Error of Regressions in the American Economic Review", Journal of Socio-Economics, 33 (5), 527–546, doi: 10.1016/j.socec.2004.09.024.]
- ↑ McCloskey, Deirdre N.; Stephen T. Ziliak (2008). The Cult of Statistical Significance: How the Standard Error Costs Us Jobs, Justice, and Lives (Economics, Cognition, and Society). The University of Michigan Press. ISBN 0472050079.
- ↑ McCloskey, Deirdre (2008). The Cult of Statistical Significance. Ann Arbor: University of Michigan Press. ISBN 0472050079.
- ↑ Wallace, Brendan; Alastair Ross (2006). Beyond Human Error. Florida: CRC Press. ISBN 978-0849327186.
- ↑ Goodman S (1999). "Toward evidence-based medical statistics. 1: The P value fallacy.". Ann Intern Med 130 (12): 995–1004. PMID 10383371. http://www.annals.org/cgi/pmidlookup?view=long&pmid=10383371.
- ↑ Goodman S (1999). "Toward evidence-based medical statistics. 2: The Bayes factor.". Ann Intern Med 130 (12): 1005–13. PMID 10383350. http://www.annals.org/cgi/pmidlookup?view=long&pmid=10383350.
- ↑ Harlow, Lisa Lavoie; Stanley A. Mulaik; James H. Steiger (1997). What If There Were No Significance Tests?. Mahwah, N.J.: Lawrence Erlbaum Associates Publishers. ISBN 978-0-8058-2634-0.
- ↑ Rosnow, R.L.; Rosenthal, R. (October 1989). "Statistical procedures and the justification of knowledge in psychological science". American Psychologist 44 (10): 1276–1284. doi:10.1037/0003-066X.44.10.1276. ISSN 0003-066X. http://ist-socrates.berkeley.edu/~maccoun/PP279_Rosnow.pdf.
- ↑ 23.0 23.1 Loftus, G.R. (1991). "On the tyranny of hypothesis testing in the social sciences". Contemporary Psychology 36: 102–105.
- ↑ 24.0 24.1 Cohen, Jacob (December 1990). "Things I have learned (so far)". American Psychologist 45 (12): 1304–1312. doi:10.1037/0003-066X.45.12.1304. ISSN 0003-066X.
- ↑ Weiss, Neil A. (1999). Introductory Statistics (5th ed.). Reading, Mass.: Addison Wesley isbn=0-201-59877-9. p. 521.
- ↑ Ioannidis, John P. A. (July 2005). "Contradicted and initially stronger effects in highly cited clinical research". JAMA 294 (2): 218–28. doi:10.1001/jama.294.2.218. PMID 16014596. http://jama.ama-assn.org/cgi/content/full/294/2/218.
- ↑ 27.0 27.1 Ioannidis, John P. A. (August 2005). "Why most published research findings are false". PLoS Med. 2 (8): e124. doi:10.1371/journal.pmed.0020124. PMID 16060722.
- ↑ Gigerenzer, Gerd (2004). "Mindless statistics". The Journal of Socio-Economics 33 (5): 587–606. doi:10.1016/j.socec.2004.09.033.
- ↑ Cohen, Jacob (December 1994). "The earth is round (p < .05)". American Psychologist 49 (12): 997–1003. doi:10.1037/0003-066X.49.12.997.
- ↑ Jones LV, Tukey JW (December 2000). "A sensible formulation of the significance test". Psychol Methods 5 (4): 411–4. doi:10.1037/1082-989X.5.4.411. PMID 11194204. http://content.apa.org/journals/met/5/4/411.
- Lehmann E.L. (1992) Introduction to Neyman and Pearson (1933) On the Problem of the Most Efficient Tests of Statistical Hypotheses. In: Breakthroughs in Statistics, Volume 1, (Eds Kotz, S., Johnson, N.L.), Springer-Verlag. ISBN 0-387-94037-5 (followed by reprinting of the paper)
- Neyman, J., Pearson, E.S. (1933) On the Problem of the Most Efficient Tests of Statistical Hypotheses. Phil. Trans. R. Soc., Series A, 231, 289–337.
External links
- Wilson González, Georgina; Karpagam Sankaran (September 10, 1997). "Hypothesis Testing". Environmental Sampling & Monitoring Primer. Virginia Tech. http://www.cee.vt.edu/ewr/environmental/teach/smprimer/hypotest/ht.html.
- Bayesian critique of classical hypothesis testing
- Critique of classical hypothesis testing highlighting long-standing qualms of statisticians
- Dallal GE (2007) The Little Handbook of Statistical Practice (A good tutorial)
- References for arguments for and against hypothesis testing
- Statistical Tests Overview: How to choose the correct statistical test
- An Interactive Online Tool to Encourage Understanding Hypothesis Testing
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


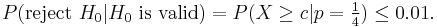



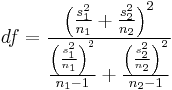
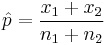
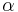 , the
, the 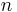 = sample size
= sample size = sample 1 size
= sample 1 size = sample 2 size
= sample 2 size = sample mean
= sample mean = hypothesized
= hypothesized  = population 1 mean
= population 1 mean = population 2 mean
= population 2 mean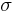 =
= 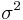 =
=  = sample standard deviation
= sample standard deviation =
=  = sample 1 standard deviation
= sample 1 standard deviation = sample 2 standard deviation
= sample 2 standard deviation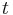 = t statistic
= t statistic = degrees of freedom
= degrees of freedom = sample mean of differences
= sample mean of differences = hypothesized population mean difference
= hypothesized population mean difference = standard deviation of differences
= standard deviation of differences = x/n = sample proportion, unless specified otherwise
= x/n = sample proportion, unless specified otherwise = hypothesized population proportion
= hypothesized population proportion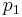 = proportion 1
= proportion 1 = proportion 2
= proportion 2 = hypothesized difference in proportion
= hypothesized difference in proportion = minimum of n1 and n2
= minimum of n1 and n2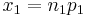

 = Chi-squared statistic
= Chi-squared statistic = F statistic
= F statistic